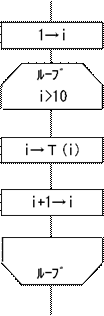流れ図の書き方（表操作）

日常生活の中でも我々は、よく表なるものを見かける。

例えば、時刻表、日程表、成績表、売上実績表、…………

コンピュータ処理に於いても、この表の概念を導入して効率的なデータ処理が行えるようにしている。

尚、コンピュータ用処理記述言語によって呼称が違いますが、表(Table)又は、配列(Array)と呼んでいる。

表を構成している一つ一つのデータ項目を表要素(Table-Element)と言う。

この表要素を参照等する場合に添字(Subscript)又は指標(Index)を用いる。

1

2

3

4

5

6

7

8

9

10

→

表の大きさは、１０

25

36

11

32

81

15

52

77

18

64

←

表要素名：Ｘ

Ｘ(1)

Ｘ(10)

この様に表要素名に()を付けて、その()の中に表の何番目かを示す為の添字を記述する。

添字とは、代数的に表現したＸiのiを示している。このＸiをＸ(i)と表しているだけです。

また、表には上図の様な一次元の表だけでなく

1

2

3

4

5

6

7

8

9

10

→

表の大きさは、１０×３

1

25

36

11

32

81

15

52

77

18

64

←

表要素名：Ｙ

2

18

42

35

64

88

69

72

49

33

27

3

84

67

36

45

21

19

48

56

42

23

Ｙ(3,2)

Ｙ(10,3)

の様に二次元の表もあり、更に三次元以上の表も取り扱うことが出来ます。

二次元の場合、表は、行と列で表現できるので、通常、横方向を行、縦方向を列と呼んでいる。（代数の行列）

例題．大きさが５の一次元の表Ｔの各要素に値０を保存する。

０→Ｔ(1)

０→Ｔ(2)

０→Ｔ(3)

０→Ｔ(4)

０→Ｔ(5)

この様にそれぞれの要素に値を保存する式を記述するとなると大きな表を扱うのは大変である。

この様な表を取り扱うために添字を変数にして繰り返し処理で表す事が出来るようになっている。

例えば、ＢＡＳＩＣ言語では、

for i = 1 to 5

T(i) = 0

next i

の様に記述する事で表Ｔの各要素に値０が保存できる。

この様な記述であれば表の大きさに依存しないので、各言語で同様の記述が出来るようになっています。

補足．二次元の表Ｘ(m,n)とＸ(n,m)とは表全体の大きさ(m×n)は同じですが、要素の並びは違います。

この要素の並びは、使用する言語で決められています。

行→列の場合

列→行の場合

Ｘ(m,n)の要素の並び

Ｘ(n,m)の要素の並び

Ｘ(m,n)の要素の並び

Ｘ(n,m)の要素の並び

Ｘ(1,1)

Ｘ(1,1)

Ｘ(1,1)

Ｘ(1,1)

Ｘ(2,1)

Ｘ(2,1)

Ｘ(1,2)

Ｘ(1,2)

Ｘ(m,1)

Ｘ(n,1)

Ｘ(1,n)

Ｘ(1,m)

Ｘ(1,2)

Ｘ(1,2)

Ｘ(2,1)

Ｘ(2,1)

Ｘ(2,2)

Ｘ(2,2)

Ｘ(2,2)

Ｘ(2,2)

Ｘ(m,2)

Ｘ(n,2)

Ｘ(2,n)

Ｘ(2,m)

Ｘ(1,3)

Ｘ(1,3)

Ｘ(3,1)

Ｘ(3,1)

Ｘ(m,n)

Ｘ(n,m)

Ｘ(m,n)

Ｘ(n,m)

流れ図の書き方（表操作）

表操作を流れ図で記述する場合には、繰り返し処理の終了条件の表し方を工夫しています。

（例）大きさ１０の一次元の表Ｔの各要素に値をＴ(1)=1,Ｔ(2)=2,Ｔ(3)=3,……,Ｔ(10)=10の様に

ｉ番目の要素に値ｉを保存する。

終了条件「i=1 TO 10」は、ｉの初期値が１で最大１０迄１ずつ増やしながら繰り返す事を表す。

（終了条件ではなく、繰り返しの有効範囲を示す。）

尚、増分値（＋でも－でも可）が１以外の場合は、その増分値も含めて表します。

（例）初期値２で２ずつ増やしながら２０迄繰り返す。

（例）初期値100で２ずつ減らしながら０迄繰り返す。

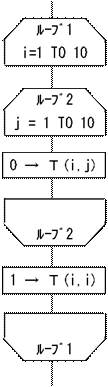
二次元の場合には、繰り返し処理が二重になります。

（例）大きさ１０×１０の二次元の表Ｔに値を以下の様に保存する。

・

Ｔ(i,i)=1　但し1≦i≦10

・

Ｔ(i,j)=0　但しi≠jで1≦i≦10,1≦j≦10

内側の繰り返し範囲

外側の繰り返し範囲